Q1: Explain the formation of interference fringes in an air-wedge shaped film. How is the thickness of the wire determined by this method?

(i) Formation of Interference Fringes (Air Wedge)

An air wedge is a thin film of air with zero thickness at one end and progressively increasing thickness at the other. This is typically formed by placing a thin object, like a wire, between two optically flat glass plates at one end.

• When monochromatic light (e.g., from a sodium vapour lamp) falls on the wedge-shaped film, it gets partly reflected from the top surface of the air film (Ray 1) and partly transmitted, then reflected from the bottom surface of the air film (Ray 2).
• These two reflected rays (Ray 1 and Ray 2) are coherent, as they originate from the same source.
• A phase change of 180° (or π) occurs for Ray 2, as it reflects from the denser medium (the top surface of the bottom glass plate). No phase shift occurs for Ray 1, which reflects from the rarer medium (the bottom surface of the top glass plate).
• This inherent 180° phase difference between the two rays is the reason they interfere destructively at thepoint of contact (where thickness is zero), forming a dark fringe.
• As the thickness 't' increases, the path difference (2t) also increases, leading to a pattern of alternate bright and dark straight-line fringes.

(ii) Determination of Thickness of Wire

The air wedge setup can be used to measure the thickness (t) of a very small object, like a thin wire.

1. Setup: Two optically plane glass plates are placed one over the other. The wire (specimen) is inserted between them at one end, and the other end is tied with a rubber band to form a wedge.
2. Illumination: Light from a sodium vapour lamp is made to fall normally on the wedge using a glass sheet held at a 45° angle.
3. Observation: The interference fringes are observed through a microscope.
4. Measurement: The horizontal positions of several dark fringes (e.g., n, n+5, n+10) are measured. From this, the average width of 5 or 10 fringes is calculated (let's say x = 5β). The fringe width (β) is then found by β = x / 5.
5. Calculation: The thickness of the wire (t) is related to the fringe width (β), the wavelength of light (λ), and the length of the air wedge (L) by the formula:

By rearranging this formula, we can determine the thickness of the wire:

Thus, by measuring the fringe width (β) and knowing λ and L, the thickness 't' of the wire can be calculated.

Q2: Describe the construction of a Michelson interferometer and discuss the different type of interference fringes formed in it.

(i) Principle and Construction

Principle: The Michelson Interferometer produces an interference pattern by splitting a beam of light into two parts. These two beams travel different optical paths and are then recombined to interfere. This method is known as "division of amplitude".

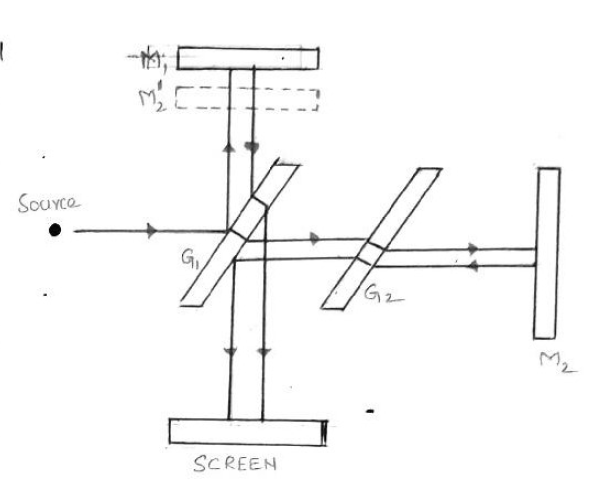
Construction: The main components are:

• Beam Splitter (G₁): A glass plate that is semi-silvered or partially polished on its rear side. It is placed at a 45° angle to the incoming light. Its function is to split the source light into two beams of equal intensity: one reflected and one transmitted.
• Compensatory Plate (G₂): An identical glass plate placed parallel to G₁. It is placed in the path of the transmitted beam to ensure that both beams (the reflected one and the transmitted one) travel through the same thickness of glass.
• Movable Mirror (M₁): A highly polished, movable mirror.
• Fixed Mirror (M₂): A highly polished, fixed mirror.
• Source: A monochromatic light source.
• Screen: A screen or telescope to observe the interference fringes.

Light from the source hits G₁. Part of it is reflected towards M₁. The other part is transmitted through G₁ and G₂ towards M₂. The beams reflect from M₁ and M₂, return to G₁, and are recombined to travel towards the screen, where they interfere.

(ii) Types of Fringes

The type of fringe pattern observed depends on the alignment of the mirrors M₁ and M₂ (which is equivalent to the air film between M₁ and the virtual image of M₂).

• Circular Fringes: These are observed when the mirrors M₁ and M₂ are perfectly parallel to each other.
• Curved Fringes: When M₁ and M₂ are inclined to each other, the air film enclosed is wedge-shaped. This arrangement produces curved fringes.
• Straight Fringes: When the mirrors M₁ and M₂ are made to intersect, straight-line fringes are obtained.

Q3: Explain the principle, construction, and working of an Nd-YAG laser. List out the advantages and applications of Nd-YAG laser.

The Nd-YAG (Neodymium-doped Yttrium Aluminium Garnet) laser is a four-level, solid-state laser.

(i) Principle

The active medium is an Nd-YAG rod. This rod is optically pumped by a krypton flash tube. The pumping raises the Neodymium ions (Nd³⁺) to higher energy levels. Population inversion is achieved in a metastable state. The subsequent transition from this metastable state to a lower energy state results in a laser beam of wavelength 1.06 μm.

(ii) Construction

• Active Medium: A cylindrical rod of Yttrium Aluminium Garnet (Y₃Al₅O₁₂) crystal, in which a small amount of Yttrium ions (Y³⁺) are replaced by Neodymium ions (Nd³⁺). The ends of the rod are highly polished and parallel.
• Pumping Source: A krypton flash tube is used for optical pumping.
• Optical Resonator: This consists of two mirrors. One mirror (M₁) is fully reflecting, and the other (M₂) is partially reflecting. In some designs, the polished ends of the rod itself can act as the resonator.
• Reflector Cavity: The laser rod and flash tube are placed inside an elliptical reflector cavity to ensure that most of the light from the flash tube is focused onto the rod.

(iii) Working

1. Pumping: When the krypton flash tube is turned on, it emits light (wavelengths 0.73 μm and 0.80 μm). The Nd³⁺ ions in the ground state (E₀) absorb this energy and are excited to upper energy levels (pump bands E₃ and E₄).
2. Population of Metastable State: From these high-energy pump bands, the Nd³⁺ ions quickly decay to a lower, metastable state (E₂) through a non-radiative transition.
3. Population Inversion: Because E₂ is a metastable state (long lifetime), ions accumulate here, achieving population inversion between state E₂ and a lower state E₁.
4. Stimulated Emission: An Nd³⁺ ion makes a spontaneous transition from E₂ to E₁, emitting a single photon. This photon travels through the rod and triggers other excited ions in state E₂ to emit identical photons (stimulated emission).
5. Amplification: These photons reflect back and forth between the resonator mirrors (M₁ and M₂), multiplying rapidly as they cause more stimulated emissions.
6. Laser Output: The beam grows in strength until an intense, coherent laser of wavelength 1.06 μm (infra-red) is emitted through the partially reflecting mirror M₂. The ions then return from E₁ to the ground state E₀ via another non-radiative transition.

(iv) Advantages and Applications

Advantages:

• It has a high energy output.
• Population inversion is much easier to achieve (a characteristic of four-level lasers).

Applications:

• Used in range finders and illuminators.
• Widely used in industry for micro-machining operations, such as welding, drilling, resistor trimming, and scribing.

Q4: Explain the modes of vibrations of CO2 molecule. Explain the construction, functioning, and application of CO2 laser with necessary diagrams.

The CO₂ laser is a four-level molecular gas laser, one of the most efficient types. Laser transitions occur between the vibrational energy states of the CO₂ molecule.

(i) Modes of Vibration of CO2

A CO₂ molecule (O-C-O) has three independent modes of vibration:

1. Symmetric Stretching: The carbon atom is stationary, while both oxygen atoms vibrate simultaneously along the molecular axis, either moving away from or towards the carbon atom.
2. Bending: Both oxygen atoms and the carbon atom vibrate perpendicular to the molecular axis.
3. Asymmetric Stretching: The atoms vibrate asymmetrically. The two oxygen atoms move in one direction while the carbon atom moves in the opposite direction, all along the molecular axis.

(ii) Construction

• Active Medium: A gas mixture of Carbon Dioxide (CO₂), Nitrogen (N₂), and Helium (He).
• Discharge Tube: A long quartz tube (e.g., 5m long, 2.5cm diameter) containing the gas mixture.
• Pumping Source: A high-voltage DC power supply connected to terminals on the discharge tube. This causes an electrical discharge, which is the pumping method.
• Optical Resonator: Formed by two concave mirrors, M₁ (fully reflecting) and M₂ (partially reflecting), placed at the ends of the tube.
• Brewster Windows: The ends of the tube are fitted with NaCl Brewster windows, which allow the laser light to pass without reflection losses and ensure the output beam is plane-polarized.

(iii) Functioning (Working)

1. Pumping (Nitrogen): The electrical discharge excites electrons. These high-energy electrons collide with Nitrogen molecules (N₂), exciting them to a metastable vibrational state.
   N₂ + e* → N₂* + e
2. Energy Transfer (Population Inversion): The excited state of N₂ (N₂*) is very close in energy to the E₅ (asymmetric stretching) state of the CO₂ molecule. Through collisions, the energy is efficiently transferred from the excited N₂ to the CO₂ molecules.
   N₂* + CO₂ → CO₂* + N₂
   This process populates the E₅ level of CO₂, achieving population inversion relative to lower levels E₄ and E₃.
3. Laser Transitions (Stimulated Emission): Laser action occurs in two main transitions:
   • E₅ → E₄ (Symmetric Stretching): This transition is more intense and produces a laser beam of wavelength 10.6 μm.
   • E₅ → E₃ (Bending): This transition produces a laser beam of wavelength 9.6 μm.
4. Role of Helium: Helium is not directly involved in the lasing action. Its role is to conduct heat from the center of the discharge tube to the cool walls, maintaining the efficiency of the laser.

(iv) Applications

• Industrial (Material Processing): Due to its high power, it is used for welding, drilling, cutting, and soldering.
• Surgical: Widely used in neurosurgery, general surgery, and microsurgery. It acts as a "bloodless" surgical knife.
• Medical Treatment: Used in the treatment of liver and lung diseases.
• Communications: Suitable for open-air communication due to low atmospheric attenuation at its wavelength.
• Sensing: Used in remote sensing.

Q5: With proper theory and diagrams, derive Einstein’s coefficients. Also discuss its inferences.

(i) Theory: Interaction of Radiation with Matter

When radiation interacts with matter, three processes can occur. Consider an atom with two energy levels, a lower ground state E₁ (population N₁) and a higher excited state E₂ (population N₂). The energy density of the incident radiation is Q.

1. Stimulated Absorption: An atom in the ground state (E₁) absorbs an incident photon of energy hv = E₂ - E₁ and jumps to the excited state (E₂). The rate of absorption (N_ab) is proportional to the ground state population (N₁) and the radiation energy density (Q).
   N_ab = B₁₂ N₁ Q
   Where B₁₂ is the Einstein's coefficient of stimulated absorption.
2. Spontaneous Emission: An atom in the excited state (E₂) returns to the ground state (E₁) by itself, emitting a photon of energy hv. This process is independent of the external radiation field. The rate (N_sp) is proportional to the excited state population (N₂).
   N_sp = A₂₁ N₂
   Where A₂₁ is the Einstein's coefficient for spontaneous emission.
3. Stimulated Emission: An incident photon of energy hv triggers (or induces) an atom in the excited state (E₂) to return to the ground state (E₁). This process emits a *second* photon that is identical in energy, phase, and direction to the incident photon. The rate (N_st) is proportional to the excited state population (N₂) and the radiation energy density (Q).
   N_st = B₂₁ N₂ Q
   Where B₂₁ is the Einstein's coefficient for stimulated emission.

(ii) Derivation of Einstein's Coefficients

At thermal equilibrium (steady state), the total rate of upward transitions (absorption) must equal the total rate of downward transitions (spontaneous + stimulated emission).

Now, we solve for the energy density Q:

Divide the numerator and denominator by B₂₁ N₂:

From Boltzmann's distribution law, the ratio of populations at thermal equilibrium is:

Substituting this into the equation for Q:

We compare this expression with Planck's radiation formula for energy density of a black body:

By comparing equations (1) and (2), we get the relations between the Einstein's coefficients:

1. (B₁₂/B₂₁) = 1 or B₁₂ = B₂₁
2. (A₂₁/B₂₁) = 8πhν³/c³

(iii) Inferences (Conclusions)

• The probability of stimulated absorption (B₁₂) is equal to the probability of stimulated emission (B₂₁).
• The ratio of spontaneous emission to stimulated emission (A₂₁/B₂₁) is proportional to ν³ (the cube of the radiation frequency).
• This means that as the energy difference (hv) between the two states increases, spontaneous emission becomes much more dominant than stimulated emission. This is why it is difficult to achieve laser action (which requires dominant stimulated emission) at very high frequencies (e.g., X-rays).

Q6: Derive an expression for numerical aperture and acceptance angle of an optical fiber.

(i) Principle

The propagation of light through an optical fiber is based on the principle of Total Internal Reflection (TIR). An optical fiber consists of a central Core (refractive index n₁) surrounded by a Cladding (refractive index n₂), where n₁ > n₂.

For TIR to occur, light must travel from the denser medium (core) to the rarer medium (cladding). If the angle of incidence at the core-cladding interface is greater than the critical angle (φ_c), the light ray is completely reflected back into the core and propagates along the fiber.

(ii) Definitions

• Acceptance Angle (θ₀): The maximum angle of incidence at the fiber end (in the launching medium, n₀) for which the light ray can enter the fiber and still undergo total internal reflection.
• Numerical Aperture (NA): The sine of the acceptance angle (NA = sin θ₀). It represents the light-gathering ability of the fiber.

(iii) Derivation

Consider a light ray entering the fiber from a launching medium (refractive index n₀) at the maximum acceptance angle θ₀.

1. At the Fiber End (Point A): The ray refracts into the core (n₁) at an angle θ_r. Applying Snell's Law at this interface:
   n₀ sin θ₀ = n₁ sin θ_r ------- (1)
2. At the Core-Cladding Interface (Point B): The ray strikes the interface at an angle φ. From the geometry of the right triangle (ΔABC), we can see that:
   φ = 90° - θ_r
   For the ray to be *just* totally internally reflected (i.e., for θ₀ to be the *maximum* acceptance angle), the angle of incidence φ must be exactly equal to the critical angle φ_c. At the critical angle, the ray is refracted at 90° into the cladding (n₂).
   
   Applying Snell's Law at Point B:
   n₁ sin φ_c = n₂ sin 90°
   n₁ sin(90° - θ_r) = n₂ (1)
   n₁ cos θ_r = n₂
   cos θ_r = n₂/n₁ ------- (2)
3. Combining the Equations: We use the trigonometric identity sin²θ_r + cos²θ_r = 1, which gives sin θ_r = √(1 - cos²θ_r).
   
   Substitute Eq. (2) into this identity:
   sin θ_r = √(1 - (n₂/n₁)²) = √((n₁² - n₂²) / n₁²)
   Now, substitute this expression for sin θ_r back into Eq. (1):
   n₀ sin θ₀ = n₁ [ √((n₁² - n₂²) / n₁²) ]
   n₀ sin θ₀ = n₁ [ √(n₁² - n₂²) / n₁ ]
   n₀ sin θ₀ = √(n₁² - n₂²)

(iv) Final Expressions

Numerical Aperture (NA):

By definition, NA = sin θ₀. Therefore:

If the medium surrounding the fiber is air, n₀ = 1. The formula simplifies to:

Acceptance Angle (θ₀):

From the NA expression, we find the acceptance angle:

If the surrounding medium is air (n₀ = 1):